Overview: Our research blends engineering, computer science, applied mathematics, and cardiovascular medicine (more recently also respiratory flows). We use advanced computational tools in our research. Members of the lab have access to Monsoon, NAU’s high performance computing cluster, where we run most of our simulations. Our lab also has a private cluster sector in Monsoon (in addition to public HPC access to Monsoon’s entire capacity).
Scientific machine learning in biomedical flows
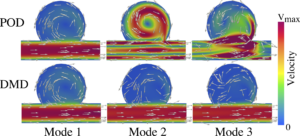
We are interested in developing data-driven and machine learning based techniques customized to unsteady biomedical flows. Current work on unsupervised machine learning approaches include models inspired by principal component analysis (PCA) and modal analysis (POD and DMD). We are also interested in developing generalized PCA models (e.g., nonlinear PCA and spectral clustering). We are also interested in developing neural network models that can assist in cardiovascular flow modeling. Current work focuses on scientific machine learning models such as physics informed neural networks (PINNs). We are also interested in autoencoders and similar neural network models that could be inspired by simpler interpretable machine learning tools.
Patient-specific computational fluid dynamics (CFD)
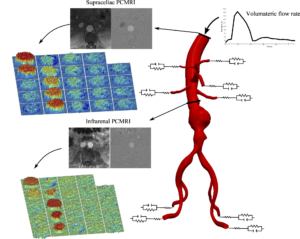
Cardiovascular disease remains the leading cause of death. We perform patient-specific and image-based CFD simulations to obtain blood flow information, which we use in studying cardiovascular disease. Computer models are typically constructed from MRI or CT data using image processing. Boundary conditions are tuned to replicate flow rates at the boundaries. These simulations are done using SimVascular, the first comprehensive open-source software package for cardiovascular flow simulation. We also frequently use Oasis and FEniCS in developing new customized CFD and mass transport models. These open-source software are used in developing multiscale and multiphysics models of disease growth.
Lagrangian wall shear stress structures
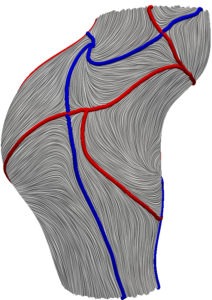
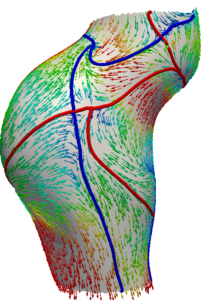
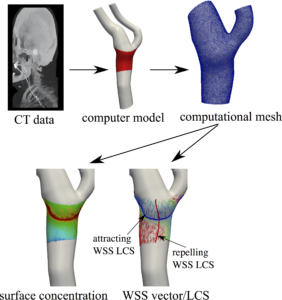
Wall shear stress (WSS) is arguably the most studied parameter in cardiovascular biomechanics. WSS quantifies the frictional drag force on the vessel wall and the endothelial cells. However, WSS also provides information on near-wall velocity. We have used this observation to study near-wall transport based on the WSS vectors. We have developed a Lagrangian surface transport model based on WSS. We have shown the emergence of Lagrangian coherent structures (LCS) in the WSS vector field. These unprecedented structures (WSS LCS) control the surface concentration patterns in cardiovascular mass transport problems. In collaboration with Dr. Guoning Chen from University of Houston-Computer Science Department, we have developed an object oriented code for Lagrangian processing of WSS data (WSS LCS, our newly proposed WSS exposure time (WSSET) measure, WSS fixed point classification, etc.).
We are also interested in exploring other potential applications for WSS LCS (such as heat transfer, turbulence, etc.).
Hemodynamics and transport in atherosclerosis
Atherosclerosis (accumulation of fatty material inside the arterial wall) is the major form of cardiovascular disease. Heart attack and stroke are consequences of this complication. We are using our novel Lagrangian WSS methodology with continuum mass transport models to study biochemical transport in atherosclerosis. The ultimate goal of this project is to build a predictive multi-scale model that can simulate the long-term progression of atherosclerosis.
Data-driven modeling with sparse representation
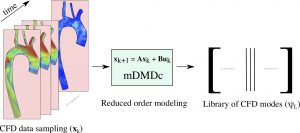
We are interested in developing physics-inspired data-driven reduced-order models in the context of diseased cardiovascular flows. We are developing dynamic mode decomposition (DMD) and proper orthogonal decomposition (POD) models for data-driven modeling of blood flow. Additionally, we are interested in using different tools in data science (e.g., machine learning and compressed sensing) to merge experimental (e.g., 4D flow MRI) and numerical techniques in characterization of cardiovascular flows. Other work include matrix completion (low-rank data recovery) and sparsity-based modeling.
Calcific aortic valve disease (CAVD)
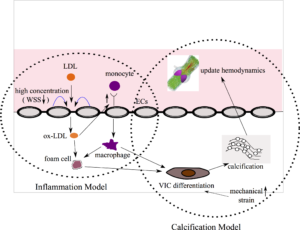
CAVD is a life-threatening disease where calcification in the aortic valve leaflets leads to incomplete opening and closure of the valve. This blocks the normal passage of blood flow from the left ventricle into the systemic circulation. In this project, we are interested in building multi-scale models that can predict the spatial and temporal progression of CAVD. This project combines several modeling techniques: nonlinear structural mechanics, fluid-structure interaction (FSI), systems biology, growth and remodeling (G&R), and multiscale modeling.
Particle transport in lung airways
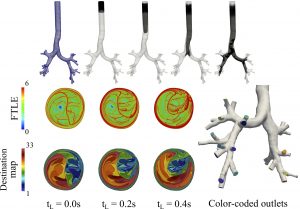
We have developed inertial particle transport models to study aerosol transport and deposition in human airways. We have shown how aerosol transport and deposition is controlled by inertial Lagrangian coherent structures (ILCS). We have shown a strong correlation between particle deposition concentration and wall shear stress divergence. We have validated laminar and turbulent flow simulations with magnetic resonance velocimetry (MRV).
Abdominal aortic aneurysm (AAA)
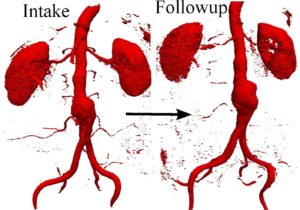
Abdominal aortic aneurysm (AAA) is the enlargement of the aorta in the abdominal level, which is a leading cause of death in the elderly. We have studied the chaotic flow topology, mixing, and transport in AAAs. We have also looked into how exercise affects the flow topology and mixing. We have correlated hemodynamics to AAA enlargement and intraluminal thrombus (ILT) deposition using longitudinal clinical data. Currently, we are interested in using new imaging techniques to correlate hemodynamics to inflammation at the wall.
Lagrangian post-processing of hemodynamics
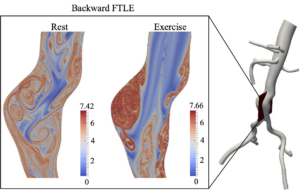
Complex anatomy and the pulsatile nature of blood flow often lead to chaotic flow in large diseased arteries. We use different Lagrangian methods for post-processing hemodynamics data. These include Lagrangian particle tracking, finite-time Lyapunov exponent (FTLE), Lagrangian coherent structures (LCS), particle residence time, and mechanical cell damage potential (stress history).
